Interpolación

 Interpolación

En el campo de las matemáticas y la informática, la interpolación es una herramienta poderosa que nos permite estimar valores intermedios entre datos conocidos. Ya sea en análisis de datos, gráficos o modelado, la interpolación desempeña un papel crucial. En esta entrada, exploraremos qué es la interpolación, por qué es importante y cómo se utiliza en diversos contextos.

¿Qué es la Interpolación?

La interpolación es un concepto matemático que se utiliza para estimar valores intermedios entre puntos de datos conocidos. En esencia, se trata de construir una función o curva suave que pase a través de los puntos dados. Esto nos permite predecir valores en lugares donde no tenemos datos exactos. Imagina que tienes puntos en un gráfico y deseas conocer el valor en algún punto entre esos puntos. La interpolación te permite hacer precisamente eso.

Métodos Comunes de Interpolación

  • Interpolación Lineal:  Es el método más sencillo y consiste en conectar dos puntos con una línea recta. Se utiliza cuando los datos siguen una tendencia lineal.
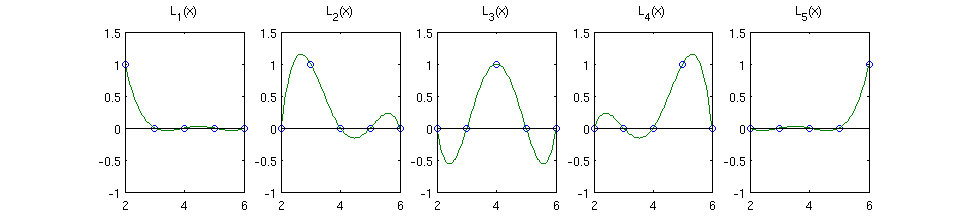
  • Interpolación Polinómica:  Se utiliza para ajustar un polinomio a través de los puntos de datos. Puede ser realizado utilizando polinomios de Lagrange o de Newton. Este método es útil para ajustar curvas más complejas.


  • Interpolación Splines: Los splines son curvas suaves compuestas por segmentos polinómicos. Se utilizan para crear una curva suave que pasa a través de todos los puntos de datos, minimizando cambios bruscos entre segmentos.


Aplicaciones Prácticas

  • Gráficos y Visualización:  La interpolación es esencial en la representación gráfica de datos, ya que ayuda a suavizar las curvas y hacer que los gráficos sean más legibles.
  • Ingeniería y Ciencias de la Computación:  Se utiliza en simulaciones y modelado para predecir comportamientos entre puntos de datos reales.
  • Procesamiento de Imágenes:  La interpolación se emplea para aumentar el tamaño de imágenes sin perder calidad aparente.
  • Análisis de Datos:  Ayuda a rellenar valores faltantes en conjuntos de datos incompletos, permitiendo análisis más completos.

Consideraciones y Desafíos:

Error de Interpolación: Es importante entender que la interpolación no siempre es perfecta y puede introducir errores, especialmente si se elige un método inadecuado o si los datos son ruidosos.

Selección del Método: La elección del método de interpolación depende de la naturaleza de los datos y la precisión requerida. Utilizar un método inapropiado puede generar resultados poco realistas.

Sobrealimentación (Overfitting): Al usar polinomios de alto grado, existe el riesgo de ajustar demasiado los datos, lo que puede llevar a predicciones inexactas fuera del rango de puntos conocidos.

Comentarios

Publicar un comentario

Entradas populares de este blog

Implementación de los Métodos Numéricos

Imagen
Implementación de los métodos numéricos La mejor forma de entender los métodos numéricos es aplicarlos directamente mediante la programación informática, ya que de esta manera podremos entender cómo funcionan. Aplicar métodos numéricos sin entender cómo funcionan es la vía más rápida a los resultados erróneos o soluciones incorrectas, ya que no se tiene una idea clara de lo que el software está haciendo con los datos. Para implementar un método numérico es fundamental escribir todos los pasos en un algoritmo, y luego, llevar dicho algoritmo a cálculos matemáticos en un programa informático que pueda ser re-utilizable para crear una simulación eficiente. Para llevar esto a cabo, es necesario tener una  metodología para desarrollar la simulación  que requerimos, mediante el uso del método numérico. Análisis numérico Expresiones matemáticas complejas requieren el uso de métodos numéricos para una respuesta aproximada. Imagen de  stimulate El análisis numérico de algoritmos s...
Leer más

Regresión Lineal y Múltiple: Modelando Relaciones y Haciendo Predicciones

Imagen
La regresión lineal y la regresión lineal múltiple son poderosas herramientas estadísticas utilizadas para analizar y modelar relaciones entre variables. Estas técnicas no solo ayudan a comprender mejor los datos, sino que también permiten hacer predicciones basadas en observaciones pasadas. En este artículo, exploraremos en qué consisten estas dos técnicas y cómo se aplican en el análisis de datos. Regresión Lineal: Entendiendo la Relación Básica La regresión lineal es una técnica que busca modelar la relación entre una variable dependiente y una sola variable independiente. La idea central es encontrar la línea recta que mejor se ajuste a los datos observados, minimizando la distancia entre los valores reales y los valores predichos por la línea. La fórmula de la regresión lineal simple es: y representa la variable dependiente que queremos predecir. x es la variable independiente, también conocida como predictor. a es la pe...
Leer más

Introducción y Conceptos Básicos

Imagen
Los métodos numéricos son algoritmos simples que se aplican para resolver diversos tipos de problemas como 1.  Interpolación . Se tiene una tabla de datos (variable independiente x, variable dependiente f(x)), se requiere conocer un valor que no se encuentra en la tabla. Si usamos un polinomio único que toca todos los puntos tabulados, estamos usando la técnica de inteporlación, distinto a la regresión donde se obtiene un polinomio que minimiza la distancia entre los puntos y el polinomio. El dato que se desea interpolar debe estar en el dominio de las x’s. El ajustar un polinomio que toque todos los puntos puede generar oscilaciones importantes y se pueden obtener resultados inesperados, fuera del contexto del problema, en estos casos se recomienda utilizar trazadores o splines, pueden ser lineales, cuadráticos o incluso cúbicos, ésta técnica asegura que la oscilación entre los puntos no sea mayor del grado del trazador. 2.  Funciones no lineales . Es común escuchar la expres...
Leer más